lecture_notes:06-01-2015
Table of Contents
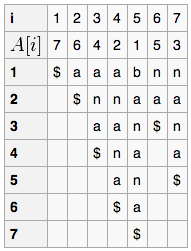
Suffix Arrays
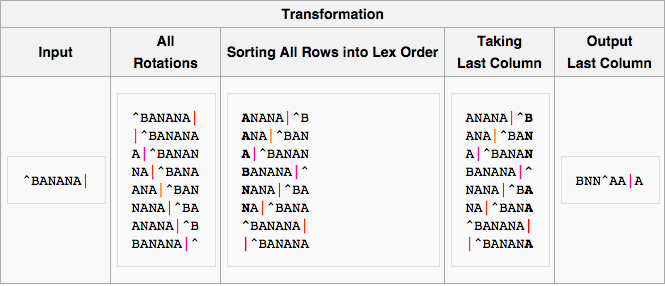
Burrows Wheeler Transform
FM Index
An FM-index is created by first taking the Burrows-Wheeler transform (BWT) of the input text. For example, the BWT of the string T = “abracadabra” is “ard$rcaaaabb”, and here it is represented by the matrix M where each row is a rotation of the text that has been sorted. The transform corresponds to the last column labeled L.
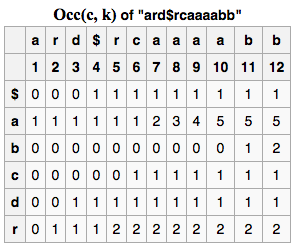
C[c] is a table that, for each character c in the alphabet, contains the number of occurrences of lexically smaller characters in the text.
The function Occ(c, k) is the number of occurrences of character c in the prefix L[1..k]
The program Bowtie uses an FM index technique
Charles M. - BWT Notes
BWA datastructure lecture
# Suffix array
# Burrows Wheeler Transform
- variation on suffix array, useful for data compression and indexing
# FM index
- uses both suffix arrays and BWT for fast lookup
suffix array definition: X[0:n] with a '$' character spliced in the range of [0,n].
e.g. string S: z a b c d e
index: 0,1,2,3,4,5
# BWT definition:
B[i] = X[S[i]-1]
1) look at suffixes of a string
a
de
cde
bcde
abcde
zabcde
2) sort order of suffixes:
Pos Suffix
6 $
1 abcde$
2 bcde$
3 cde$
4 de$
5 e$
0 zabcde$
3) rotate the string:
zabcde[$]
abcde$[z]
bcde$z[a]
.
.
.
$zabcd[e]
^
(last column is the burrows wheeler transform)
left column (since it is in alphabet order) just record where a character starts since there is
repetition of a character.
-> $
$
$
-> A
A
A
A
...
-> C
C
...
4) Record Occupancy:
Definitions:
C(a) # Where char's start.
Occ(a,i) # Array of number of char's before i in B. (e.g. # of a's in B[0,i])
- Can store part of the Occupancy array to obtain greater
compression at the cost of slightly greater cpu time.
B # BWT array
Use last_to_first(i) function which allows you to take the BWT string and find the 1st column
row index of a BWT character.
Use that row index to find the previous character in the BWT string (It's the last column
character of the same row index).
Occupancy function: C(B[i]) + Occ(B[i],i)
# Search algorithm
Given Pattern P
R(P): where pattern starts
Rbar(P): where pattern ends
Rbar(aP) = C(a) + Occ(a, Rbar(P))
R(aP) = C(a) + Occ(a,R(P)-1)+1
Additional resources and better examples can be found below:
You could leave a comment if you were logged in.
lecture_notes/06-01-2015.txt · Last modified: 2015/06/01 23:15 by jaredc